引入#

KMP算法可以求解出一个模式串在文本串中出现的位置。扩展KMP算法（Z函数）在这个思路上进行了延伸。对于文本串S的每一个后缀（如果文本串S长度为n的话，就指的是 S[i:n] ，其中 (0<=i<=n-1) ），找到这个后缀与模式串T的最长公共前缀的长度，存储在 extend[i] 中。设模式串T长度为m，不难发现，如果我们只看 extend[i] = m 的情况，相当于在文本串S找出模式串T出现的位置，就和原本的KMP算法一样了。

扩展KMP算法在国外一般叫做Z函数(Z function)。

计算extend数组#

对于模式串T，我们需要预处理一个数组 next 。其第i项表示从i开始T的后缀与T的最长公共前缀的长度。next 数组的求解在下节可以看到，我们先来看看如何用 next 数组计算出 extend 数组。

和之前说的马拉车算法类似，拓展KMP算法也是利用之前的数据对暴力算法进行优化。维护一个当前所到达过的最右边的值 right 以及所对应的起点 left （即 left + extend[left] - 1 的最大值为 right ）。此时在第 i 项，默认其前面的 extend[i-1], extend[i-2], ... extend[0] 都已经更新完毕。

如果 i > right ，说明此时第 i 项还没有更新。此时就用最简单的暴力算法向前推进，并且更新 left 和 right 的值。

1
left = i;
2
while((i+extend[i])<s.length() && (extend[i])<t.length() && t[extend[i]] == s[i+extend[i]]){//思考题：为什么这里没有+1
3
  extend[i]++;
4
}
5
right = left + extend[i] - 1

如果 i <= right ，就可以利用 left 和 right 的值来更新 extend[i] 了。

求解extend数组的最小值#

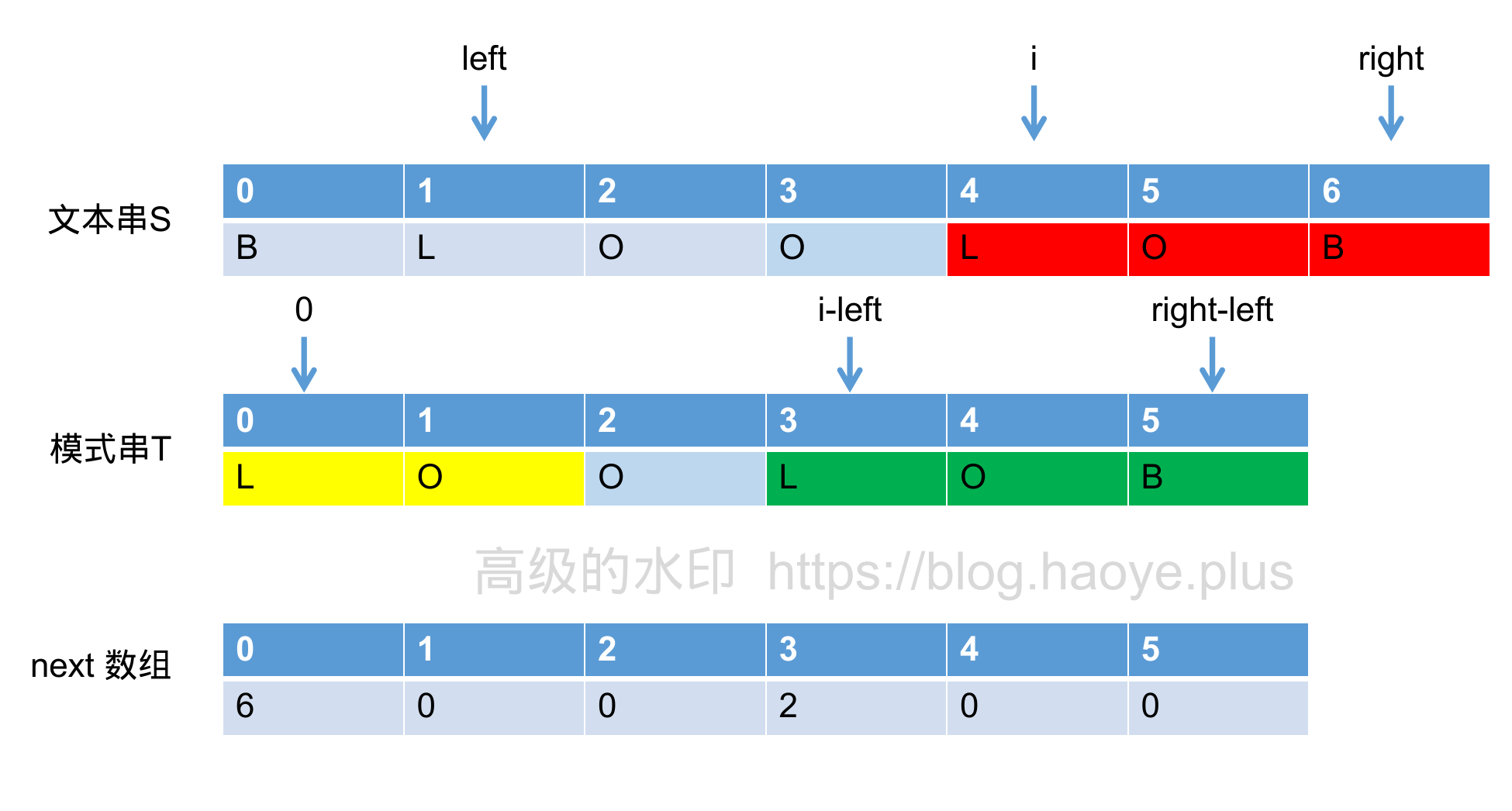
extend高级图片2

从上图结合之前学的内容可知， S[left:right+1] 和 T[0:right-left+1] 的值是相同的。也就是 S[i:right+1] 与 T[i-left:right-left+1] 的值是相同的（图中红色区域和绿色区域是相同的）。next[i-left] = 2 可以求得 T[0:2] = T[i - left:i - left + 2 + 1] 也就是黄色区域等于绿色区域的前两个。又因为红色区域等于绿色区域，所以红色区域前两个等于黄色区域。也就是文本串S以第i项开头的后缀与模式串T的最长公共前缀为2，也就是黄色区域的长度 next[i - left]。进而得到 extend[i] = next[i - left]

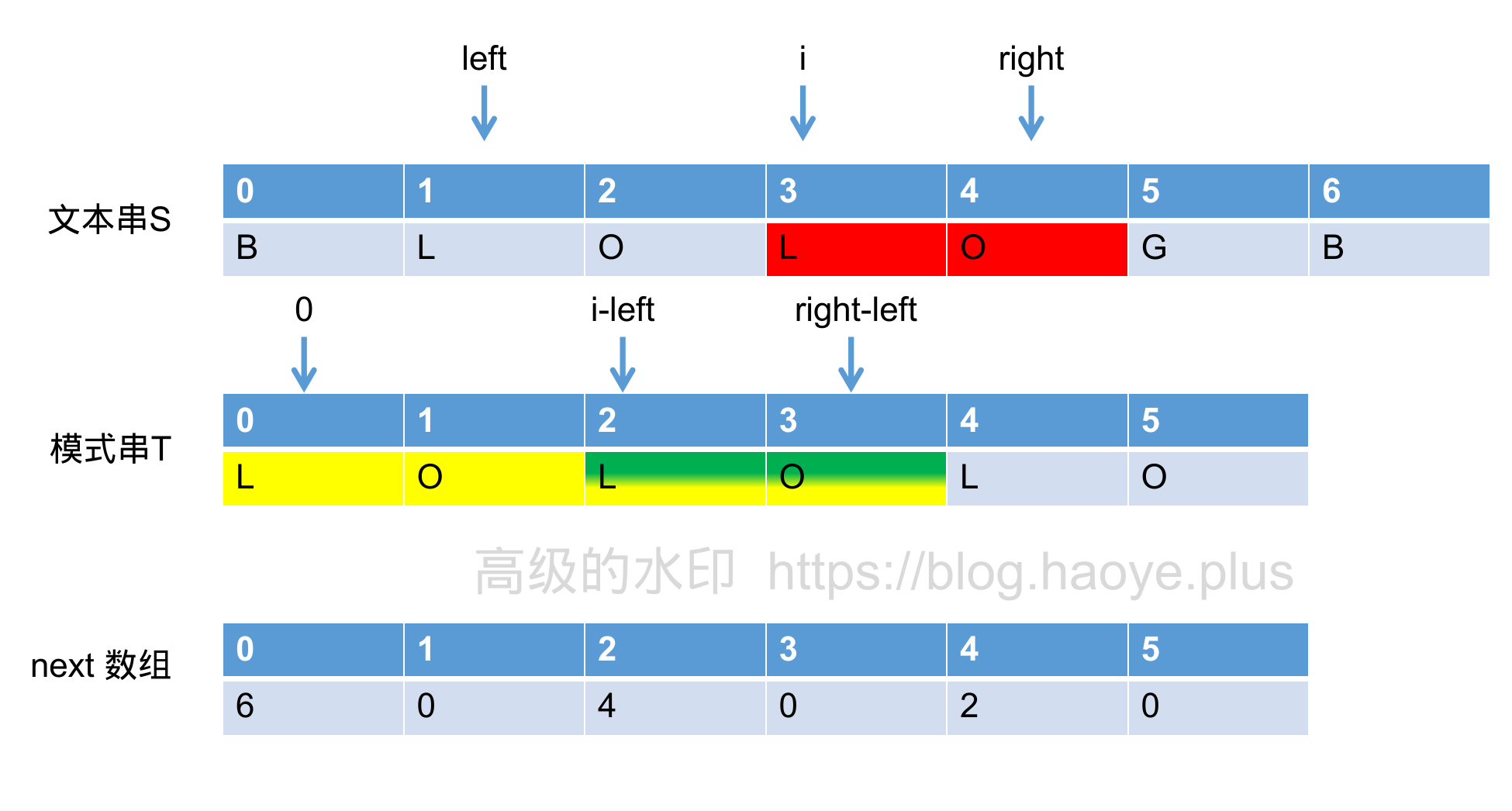
extend高级图片1

我们再来看一个例子。

根据上文所述的方法画出红色，绿色和黄色区域。我们会发现套用上一个结论行不通。因为黄色区域的长度已经超过了红色区域的长度。而我们只能保证红色区域与绿色区域相同，并不能保证红色区域的下一个值和绿色区域的下一个值相同，也就是 S[5] 和 T[4] 不能确定是否相同。此时就应该用红色区域的长度作为 extend[i] 的值。extend[i] = right - i + 1。

综上，可以得出一个通用式子。

1
extend[i] = min(right - i + 1, next[i - left]);

拓展#

如果 i + extend[i] - 1 = right ，说明本次更新已经到了 s[left:right+1] 所管辖的尽头，需要对其进行更新。此时就和暴力的时候一样就好了，拓展 extend[i] 的值并且更新 left 和 right。

1
if(i + extend[i] - 1 > right){
2
    left = i;
3
    while((i+extend[i])<s.length() && (extend[i])<t.length() && t[extend[i]] == s[i+extend[i]]){//思考题：为什么这里没有+1
4
        extend[i]++;
5
    }
6
    right = i + extend[i] - 1
7
}

next 数组#

其实和上一节很相似，只不过是文本串和模式串都是T而已。这里就直接上代码

1
void calNextt(){
2
    nextt[0] = t.length(); // 自己和自己的最长公共前缀就是自己本身
3
    int left,right;
4
    left = right = 0;
5
    for(int i=1;i<t.length();i++){
6
        if(i<=right)
7
            nextt[i] = min(right-i+1,nextt[i-left]);
8
        while((i+nextt[i])<t.length() && t[nextt[i]] == t[i+nextt[i]]){
9
            nextt[i]++;
10
        }
11
        if(i+nextt[i]-1>right){
12
            left = i;
13
            right = i+nextt[i]-1;
14
        }
15
    }
16
}

代码实践#

代码实践：洛谷P5410

不要忘了用long long!!!!（改了很久的愤怒）

1
//LICENSE: GPL v3.0
2
//https://blog.haoye.plus
3

4
#include<iostream>
5
#include<string>
6
#define int long long
7
using namespace std;
8
string s,t;
9
int nextt[20000009];//next 为保留字，不能用
10
int extend[20000009];
11

12
void calNextt();
13
void calExtend();
14

15
signed main(){
16
    cin>>s>>t;
17

18
    calNextt();
19
    //计算答案
20
    int ans = nextt[0]+1;
21
    for(int i=1;i<t.length();i++)
22
        ans = ans xor ((i+1)*(nextt[i]+1));
23
    cout<<ans<<endl;
24

25
    calExtend();
26
    //计算答案
27
    ans = extend[0]+1;
28
    for(int i=1;i<s.length();i++){
29
        ans = ans xor ((i+1)*(extend[i]+1));
30
    }
31
    cout<<ans<<endl;
32

33
    return 0;
34
}
35

36
void calNextt(){
37
    nextt[0] = t.length(); // 自己和自己的最长公共前缀就是自己本身
38
    int left,right;
39
    left = right = 0;
40
    for(int i=1;i<t.length();i++){
41
        if(i<=right)
42
            nextt[i] = min(right-i+1,nextt[i-left]);
43
        while((i+nextt[i])<t.length() && t[nextt[i]] == t[i+nextt[i]]){
44
            nextt[i]++;
45
        }
46
        if(i+nextt[i]-1>right){
47
            left = i;
48
            right = i+nextt[i]-1;
49
        }
50
    }
51
}
52

53
void calExtend(){
54
    extend[0]=0;
55
    while((extend[0])<s.length() && (extend[0])<t.length() && t[extend[0]] == s[extend[0]]){
56
        extend[0]++;
57
    }
58

59
    int left,right;
60
    left = 0;
61
    right = extend[0]-1;
62
    for(int i=1;i<s.length();i++){
63
        if(i<=right)
64
            extend[i] = min(right-i+1,nextt[i-left]);
65
        while((i+extend[i])<s.length() && (extend[i])<t.length() && t[extend[i]] == s[i+extend[i]]){
66
            extend[i]++;
67
        }
68
        if(i+extend[i]-1>right){
69
            left = i;
70
            right = i+extend[i]-1;
71
        }
72
    }
73
}