马拉车算法可以用线性级时间复杂度找出最长回文子串。

回文子串

考虑这么一种字符串，它正着读和倒着读的内容都一样。我们称这种字符串为回文串。

回文串图片

接下来的算法目的是在一个字符串的所有子串中找到一个长度最长的回文串，也就是最长回文子串。

修改回文串

根据回文串长度的奇偶性，可以将它分为两类: 长度为奇数的回文串和长度为偶数的回文串。长度为奇数的回文串中心只有一个元素，而长度为偶数的有两个。

两种回文串

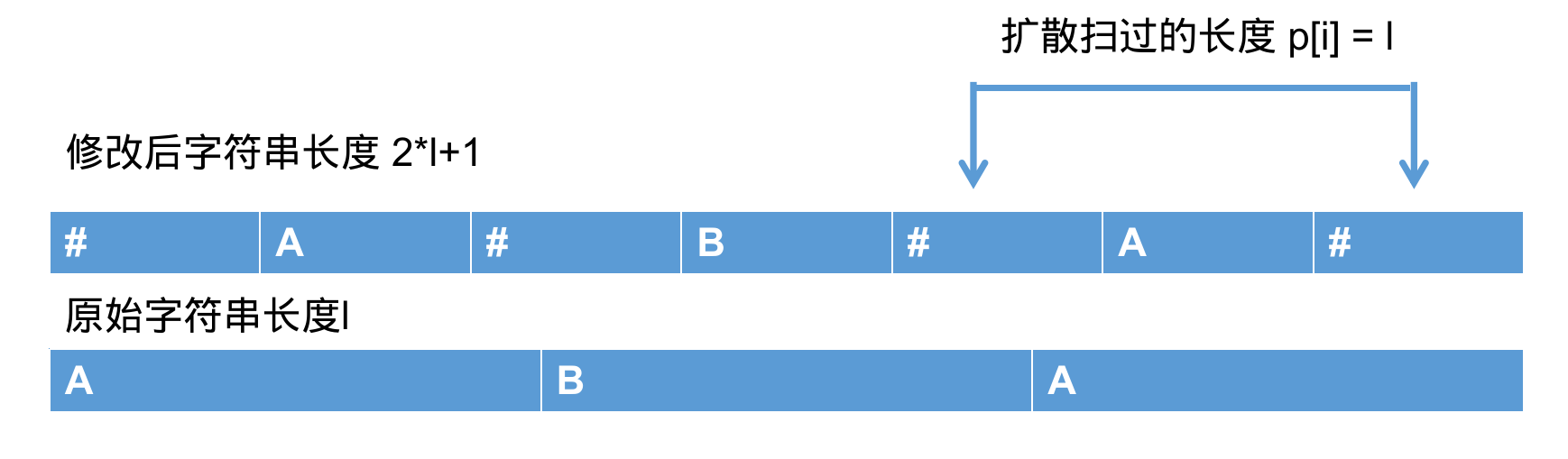
如果对于这两种回文串进行分类讨论的话，代码会变得更加复杂。我们可以在回文串的左右两边和每个字符之间加上一个特殊字符。这样就只用讨论长度为奇数的回文串。

加了特殊字符的两种回文串

O(n^2) 求解

很容易想到的一种思路就是暴力枚举。以每一个元素为回文串的中心同时向左右扩散，直到碰到边缘或者左右字符不一致时停止。这被称作中心扩散法。

#include<bits/stdc++.h>
using namespace std;
char s[22000010];
int n;
int p[22000010];
int maxx;
inline void algorithm(){
​    for(int i=0;i<n;i++){
​        //扩散
​        while(i - p[i] -1 >= 0 && i + p[i] + 1 < n && s[i+p[i]+1] == s[i-p[i]-1]){
​            p[i]++;
​        }
​        //更新最终答案
​        maxx = max(maxx,p[i]);
​    }
}
int main(){
​    //输入并添加特殊字符
​    char c;
​    c=getchar();
​    while('a'<=c && c<='z'){
​        s[n++]='#';
​        s[n++]=c;
​        c=getchar();
​    }
​    s[n++]='#';
​    maxx = 0;
​    //算法处理
​    algorithm();
​    //输出
​    cout<<maxx<<endl;
}

代码会处理添加过特殊字符后的回文串，并记录扩散次数到p数组。

我们会发现，p数组存储的值正好是对应位置修改前的原始最长回文子串的长度。这样记录好p数组的最大值就可以知道答案了。下面是简短的证明。

以某一项元素为中心扩散最终左右两边的极限一定是特殊字符。因为不等于的情况永远不是特殊字符（或者碰到边界，不过整个字符串首位就有特殊字符，所以这个情况不难证明），所以最终这个回文串的左右两边的极限肯定都为特殊字符。

对某一个元素而言，设回文串长度为 2 * l + 1, 则除去特殊字符的原始字符串长度为 l ，p[i] 也等于 l。所以相等。

p数组证明

马拉车算法思路

O(n^2)算法的时间复杂度显然不占优势。利用回文串的性质可以对它进行优化

马拉车算法会记录两个值。一个是目前所有回文子串中最靠右的右端点的下标 max_right ，另一个是它所对应的回文串中心的下表 center

在进行第一个循环时，如果所在的元素 i 的下标大于 max_right 说明目前的回文子串无法覆盖到 i 。此时就只能用到上文的扩散法计算p数组的值并更新 max_right 与 center。

可如果 i 不大于 max_right ，说明有之前的回文串可以覆盖到 i 。此时就可以利用回文串的性质进行优化了。

利用 i 关于 center 对称的元素 mirror，我们可以计算出 p[center] 的最小值。

举个例子，考虑以第9项作为center的情况

例子图片

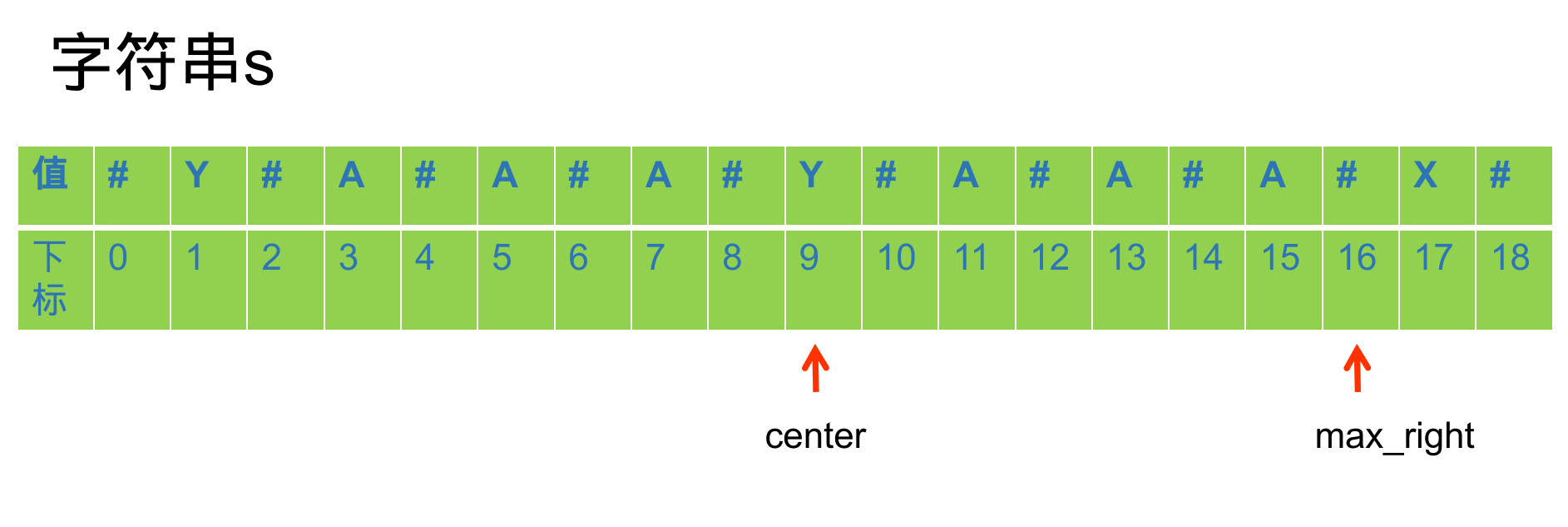
对于字符串s，可能会出现下面的三种情况。

如果 p[mirror] < max_right - i (这里 max_right - i 代表着以 center 为中心的回文串最左端离 mirror 的距离)，此时 p[i] = p[mirror]。 因为根据回文串的性质， mirror - p[mirror] 到 mirror + p[mirror] 是回文串必然能推出 i - p[mirror] 到 i + p[mirror] 子串也是回文串。s[ mirror - p[mirror] - 1 ] != s[ mirror + p[mirror] + 1 ] 也能推导出 s[ i - p[mirror] - 1 ] != s[ i + p[mirror] + 1 ]，证明这是最长的回文串。

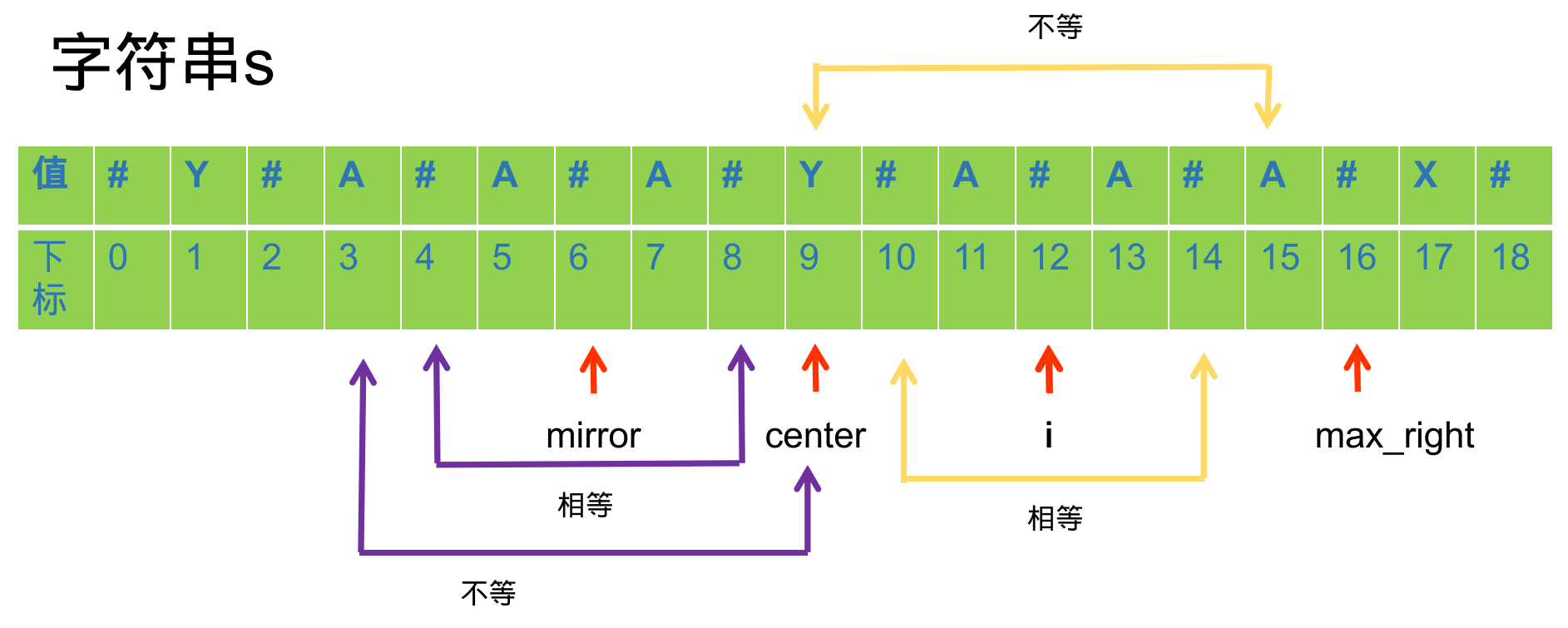
小于的情况

如果 p[mirror] = max_right - i ，同上可知 p[i] = p[mirror]。 设左端点为 left，则 s[ mirror-p[mirror]-1 ] != s[ mirror+p[mirror]+1 ] 不能推导到以 i 为中心的回文串上。所以此时需要扩散回文串并且更新 max_right 与 center。

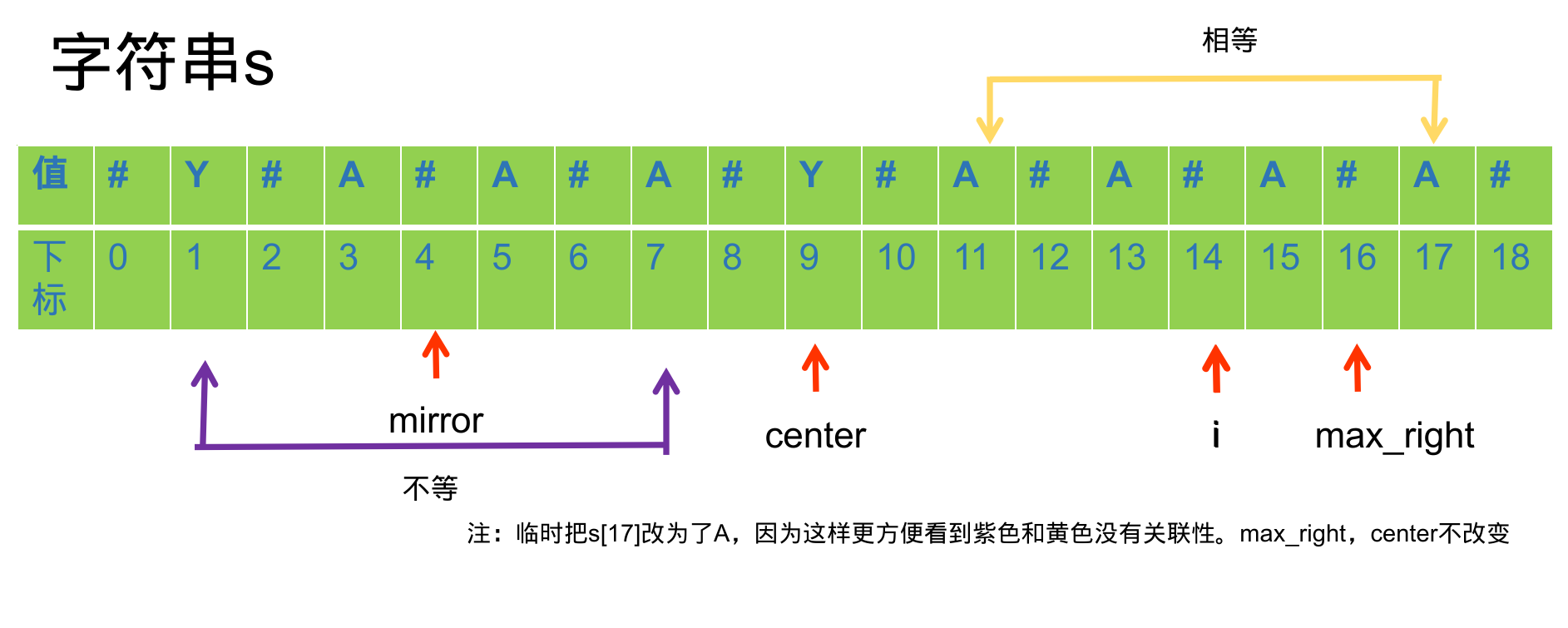
相等的情况

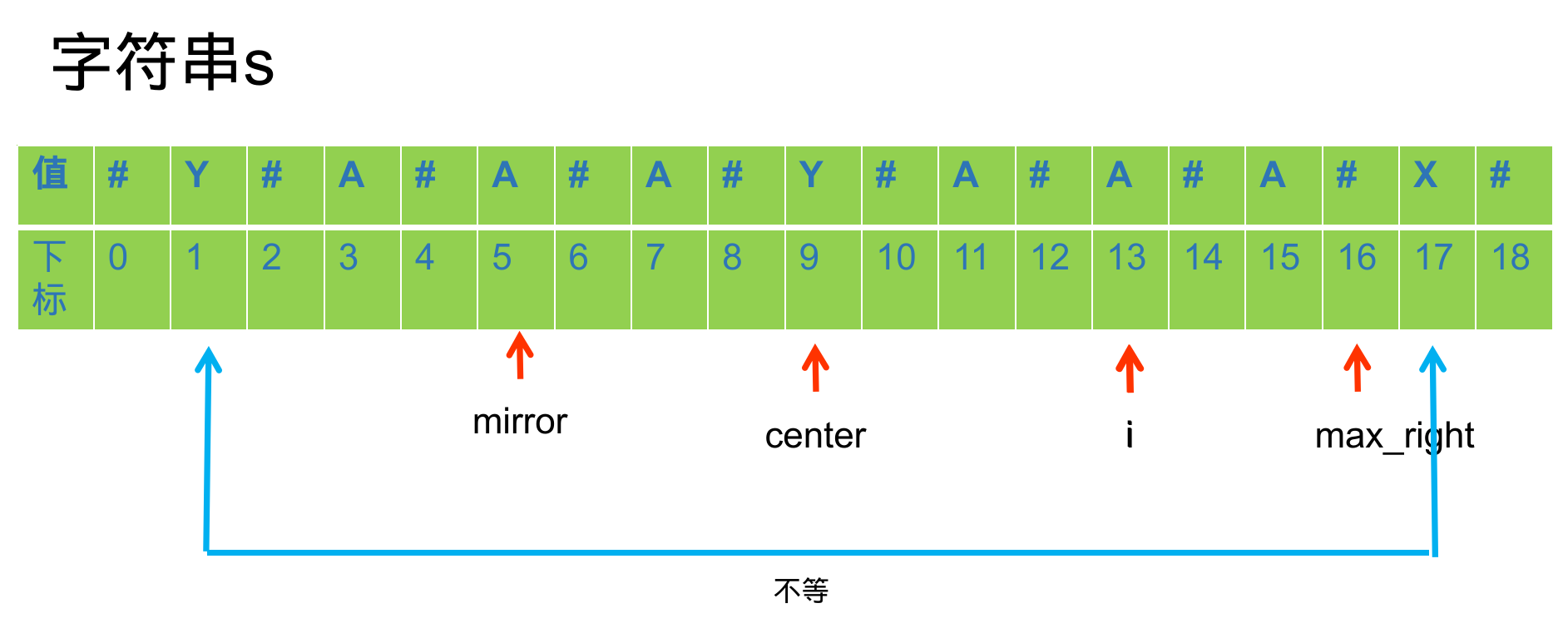
如果 p[mirror] > max_right - i ，此时以 mirror 为中心的回文串已经超出了以 center 为中心的回文串的范围。通过以 center 为中心的回文串的性质所推导出来的结论只适用于这个回文串本身的范围。对于他左端点往左和右端点往右的对称性无法保证。设左端点为 left，可得到 s[ center-p[left]-1 ] != s[ center+p[right]+1] 。因此此时 p[i] = max_right - i。

大于的情况

代码实践

模版题: P3805 马拉车

C++代码

#include<bits/stdc++.h>
using namespace std;
char s[22000010];
int n;
int p[22000010];
int maxx;
inline void manacher(){
​    int center,right;
​    center = -1;
​    right = -1;
​    for(int i=0;i<n;i++){
​        int mirror = center * 2 - i;
​        //如果i在center回文串里面
​        if (i < right){
​            p[i] = min(right - i, p[mirror]);
​        }
​        //扩散
​        while(i - p[i] -1 >= 0 && i + p[i] + 1 < n && s[i+p[i]+1] == s[i-p[i]-1]){
​            p[i]++;
​        }
​        //更新right和center
​        if(i+p[i]>right){
​            right = i+p[i];
​            center = i;
​        }
​        //更新最终答案
​        maxx = max(maxx,p[i]);
​    }
}
int main(){
​    //输入并添加特殊字符
​    char c;
​    c=getchar();
​    while('a'<=c && c<='z'){
​        s[n++]='#';
​        s[n++]=c;
​        c=getchar();
​    }
​    s[n++]='#';
​    maxx = 0;
​    //马拉车
​    manacher();
​    //输出
​    cout<<maxx<<endl;
}

封面图来源: 这里